[ 짧고 쉬운 경제 ] 화폐, 통화, 그리고 신용창조 수요/공급,소비자잉여/생산자잉여 수요/공급의 가격탄력성 비교우위/절대우위, 보호무역/자유무역 명목변수와 실질변수 한계(Marginal) 자본과 노동, 장기와 단기 저량수요와 저량공급 사유재 / 클럽재 / 공유자원 / 공공재 GDP의 산출과 Y=C+I+G+NX 외환보유고 통화정책과 기준금리 주택담보대출과 LTV / DTI / DSR 지니 계수 - 소득 불평등의 측정 브레튼우즈 체제 / 달러와 기축통화[1] 페트로달러 체제 / 달러와 기축통화[2] 플라자 합의 / 일본의 ‘잃어버린 10년’ 2008년 미국발 글로벌 금융위기 국제수지=경상수지+자본수지규모의 경제 | 범위의 경제근면 혁명기저효과낙수효과 | 분수효과대공황 | 대침체 | 대봉쇄대분기(논쟁)디폴트 | 모라토리움레몬마켓모럴 해저드맬서스 트랩베어마켓/불마켓벤포드의 법칙배출권 거래 제도시장실패/정부실패실업/실업률인플레이션/디플레이션/스태그플레이션증자/감자좌파/우파카르텔쿠즈네츠 가설케인스폰지게임필립스곡선환율휘플지수/ABCC지수FED | FRB | FOMCJ커브효과 | 마샬-러너조건PBR | PER | EV/EBITDA | ROE | EPS [ 맨큐의 경제학 ] 1부. 서론 2부. 시장의 작동 원리 3부. 시장과 경제적 후생 4부. 공공경제학 5부. 기업행동과 산업조직 6부. 노동시장의 경제학 7부. 소비자선택이론과 미시경제학... 8부. 거시경제 데이터 9부. 장기 실물경제 10부. 화폐와 물가의 장기적 관계 11부. 개방경제의 거시경제학 12부. 단기 경기변동 13부. 책 말미에 [ 미시경제학 ] [미시.1] 소비자선택이론 [미시.2] 생산자선택이론 : 생산함수 [미시.3] 생산자선택이론 : 비용함수/공급함수 [미시.4] 노동시장의 수요/공급/균형 [미시.5] 일반균형이론과 후생경제학 [ 거시경제학 ] [거시.1] 국민소득결정이론 [거시.2] IS-LM 모형 [거시.3] AD-AS 모형 [거시.4] IS-LM-BP 모형 [ 기타 / 개인적인 생각 ] 공공경제학의 의의 금융시장론 요약 유동자산총액 결정 매커니즘 환율의 정의/환율-경상수지 결정모형 고용의 개념 및 측정상의 문제 주택가격결정 모형 다양한 국제 환경 협약이 우리나라... 소비함수(절대/상대/항상) 기준금리와 국채수익률의 관계 주식, 차트 보는 방법 2021년 경제전망 (개인의 견해) 비트코인과 가상화폐 (개인의 견해) 게임스탑(GME) 주가 폭등 사건 2022년 경제전망 (개인의 견해) 중위 연령 - 늙어가는 우리나라 2022년 엔저 효과 (개인의 견해) 2023년 경제전망 (개인의 견해) 2024년 경제전망 (개인의 견해)

★ 본 포스트는 PC 에 최적화되어 있음

본 내용은 맨큐의 경제학 5부 기업행동과 산업조직의 확장판으로 생산자선택이론이며,
미시경제학 수업 내용을 중심으로 서승환교수님의 미시경제학,
위키백과, 네이버지식백과 등의 내용을 참고하여 작성한다.
★★ 이번 내용은 비용함수와 공급함수에 관련된 내용이다.

생산함수에 대한 내용은 이전 포스트를 참고하도록 한다.
◆ 생산자선택이론 – 생산함수 : 지금보기

비용함수(cost function)는 산출량과 최소비용 사이의 관계이며,
생산함수에 비해 추정하기가 쉬우며, 또한 비용함수를 알면 생산함수를 알 수 있다.

공급함수(supply function)은 가격과 공급량과의 대응관계를 나타내는 함수이며,
공급함수를 그래프로 표현한 것이 공급곡선이다.

◆ 비용함수 : 위키피디아 참고
◆ 공급함수 : 네이버지식백과 참고

※ 본 포스트는 생산자잉여에 대해서는 다루지 않는다.

■ 단기 비용함수

단기에는 장기와는 다르게 자본이 고정비용이므로 아래와 같이 표기할 수 있다.

때문에 X재를 생산하는 단기 비용함수는 아래와 같다.


그리고 위 식을 X재의 산출량(X) 으로 나누어주면
가 된다.

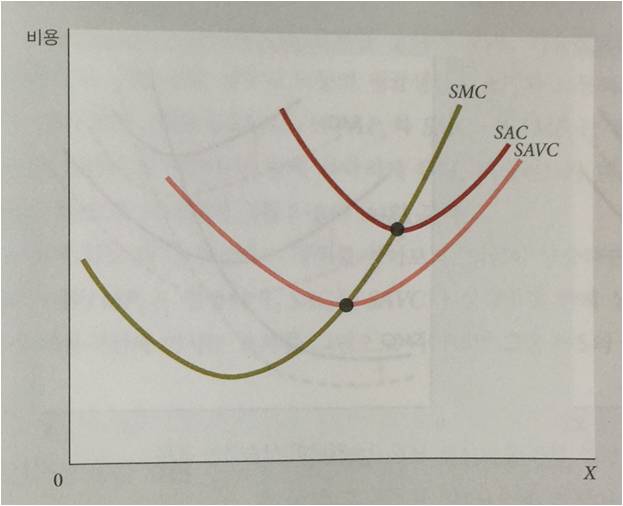
위 그래프에 표시되지 않았지만 단기 평균고정비용은 다음과 같다.

X재의 산출량이 증가함에 따라 단기평균고정비용은 감소한다.

단기 평균가변비용의 그래프는 위와 같으며, 다음와 같은 성질이 있다.

그리고 단기 한계비용의 그래프틑 위와 같으며, 다음과 같은 성질이 있다.

 

■ 장기 비용함수

장기에는 자본까지 모두 가변비용이 된다.

때문에 X재를 생산하는 장기 비용함수는 아래와 같다.

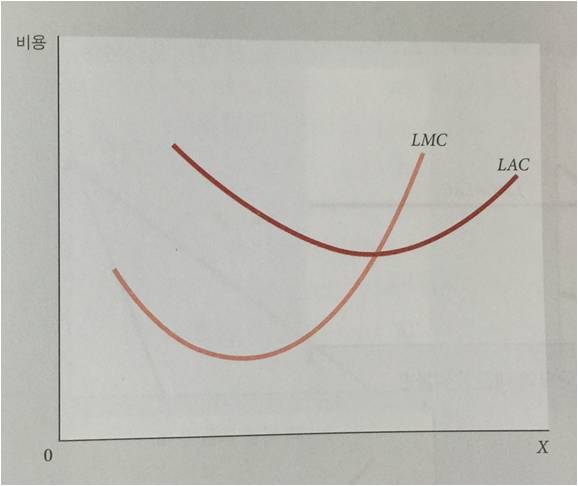
그리고 장기 평균비용, 장기 한계비용의 그래프는 위와 같고,
아래와 같은 성질을 가진다.

■ 단기와 장기 비용함수 비교

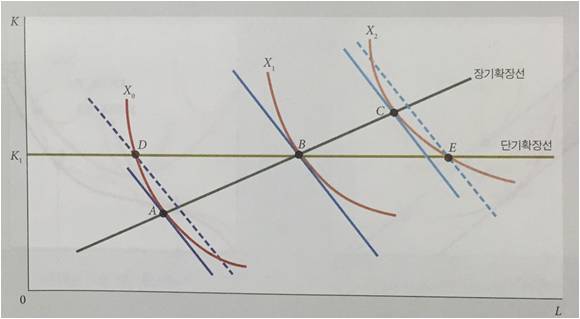
산출량을 기준으로 단기와 장기의 비용함수를 비교해보도록 한다.
★★ 다시 한번 말하지만 산출량이 기준이다.

장기에는 자본 투입량을 변화시킬 수 있기 때문에 등량곡선과 등비곡선이 접하는 요소결합을 선택할 수 있다.
때문에 산출량이 일 때 장기의 비용 극소화는 A 지점을 통해 달성할 수 있다.

하지만 단기에는 산출량이 마찬가지로 일 때, 비용 극소화는 A 지점이 아니다.
자본 투입량이 로 정해진다면 자본에 대한 지출금액은 이기에
A가 아닌 D 지점을 선택해야 비용 극소화를 이룰 수 있다.
( 이하의 자본을 투입한다고 하더라도 비용은 만큼 지불해야 하기 때문이다.)
따라서 산출량이 일 때, 단기 총비용은 장기 총 비용보다 많다.

또한 산출량이 일 때
장기에는 자본을 추가로 투입가능하므로 C 지점을 통해 비용 극소화를 이룰 수 있고,
단기에는 자본이 역시 로 정해져있으므로 E 지점을 통해 비용 극소화를 이룰 수 있다.
따라서 산출량이 일 때, 단기 총비용은 장기 총 비용보다 많다.

★★ 위 두 경우 모두 등량곡선은 장기와 단기가 동일하지만(산출량이 동일했을 때를 가정한 것이므로)
등비곡선이 단기에 더 높다는 것을 확인하면 어렵지않게 이해할 수 있다.

마지막으로 또한 산출량이 일 때는 장기와 단기가 동일한데
그 이유는 장기에 등비곡선과 등량곡선이 접하는 지점에서의 자본량이
단기에 주어진 자본량과 동일하기 때문이다. (한마디로 운이 좋은 경우)
이 경우에는 유일하게 단기 총비용과 장기 총 비용이 같다.

단기에 주어진 자본의 양이 이고, 산출량 일 때
단기 총비용과 장기 총비용이 같다면 단기 총비용과 장기 총비용의 관계는 아래와 같다.
(산출량이 일 때)

★★ 장기와 단기에 생산량이 같다면 모두 단기 총비용이 장기 총비용보다 많고,
단 하나의 생산량의 지점에서만 단기 총비용과 장기 총비용이 같다는 의미이다.
(!! 는 i번째 산출량이 아니고, 가정에 의해 주어진 상수와 마찬가지인 수이다.)

또한 단기 총비용과 장기 총비용의 위와 같은 관계는 단기 평균비용과 장기 평균비용에서도 동일하다.
(산출량이 일 때)

이러한 단기 평균비용과 장기 평균비용의 관계는 아래와 같다.

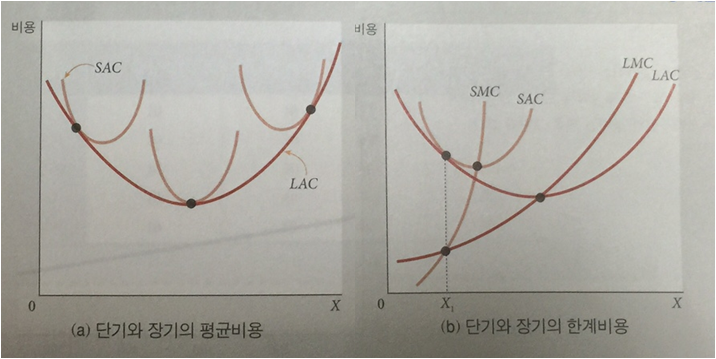
위의 내용에 따라 좌측 그래프처럼 장기 평균비용곡선은 단기 평균비용곡선의 포락선이 된다.
그리고 우측 그래프는 단기 한계비용과 장기 한계비용의 관계에 대한 내용으로
산출량이 인 지점에서 단기 평균비용과 장기평균 비용이 같다면
해당 산출량에서는 장기 한계비용과 단기 한계비용도 같다는 것을 의미한다.

그리고 장기 한계비용과 단기 한계비용은 아래와 같은 관계가 있다.
(산출량이 인 지점에서 단기 평균비용과 장기평균 비용이 같다면)

 

■ 이윤극대화

이윤극대화는 이윤을 극대화하기 위해 생산량을 어느 수준으로 정해야 하는가에 대한 문제이다.

우선 이윤은 총수입 – 총비용 으로 아래와 같이 나타낼 수 있다.

TC 는 단기에는 STC 로 표기, 장기에는 LTC 로,
TR(총수입) = P(가격) * X(산출량) 으로 볼 수 있으며,
TC(총비용) = VC(가변비용) + FC(고정비용) 으로 볼 수 있다.

또한 평균수입과 한계수입은 다음과 같이 나타낼 수 있다.

그리고 MC(한계비용)이 증가할 때
MR(한계수입) = MC(한계비용) 인 지점에서 생산한다면 이윤극대화를 이룰 수 있다.

단기에는 산출량이 다음을 만족시킬 때 이윤이 극대화된다.
( SMC(X) 가 증가하고 있는 구간에서 )

장기에는 산출량이 다음을 만족시킬 때 이윤이 극대화된다.
( LMC(X) 가 증가하고 있는 구간에서 )

★★ 장기 이윤은 단기 이윤을 초과할 수 없다.(동일 산출량, 동일 자본량이라면 같을 수는 있다.)

■ 공급함수

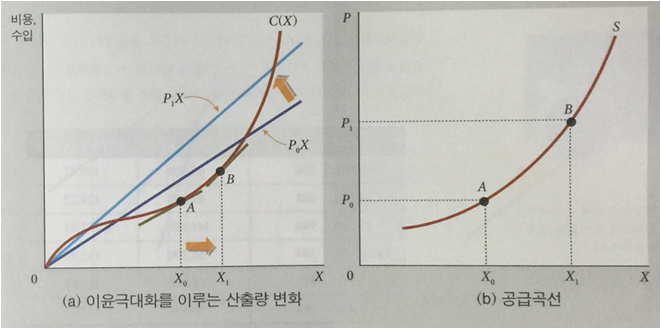
위의 (a)와 같이 총수입곡선이 직선이라면 주어진 가격 P의 수준에 따라
이윤극대화를 이루는 산출량의 수준이 달라진다.
이를 차원을 달리하여 (b)와 같이 (X, P) 평면에 그리면 공급곡선을 얻을 수 있다.

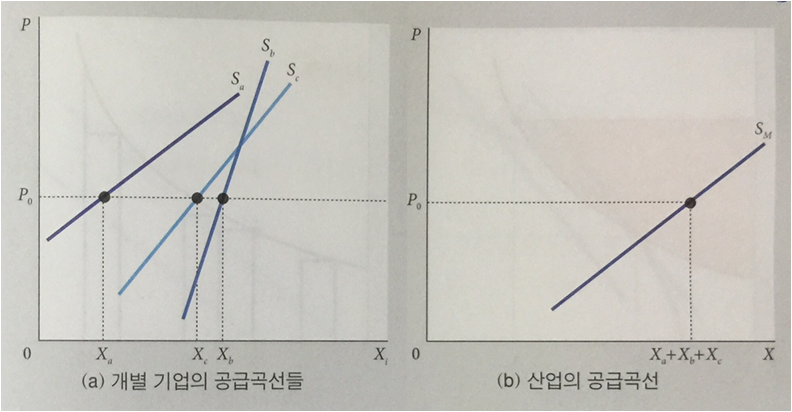
(a)와 같이 개별 기업들의 다양한 공급곡선을 수평으로 합하면 (b)와 같이 산업의 공급곡선을 얻을 수 있다.

★ 본 포스트는 PC 에 최적화되어 있음

[ 짧고 쉬운 경제 ] 화폐, 통화, 그리고 신용창조 수요/공급,소비자잉여/생산자잉여 수요/공급의 가격탄력성 비교우위/절대우위, 보호무역/자유무역 명목변수와 실질변수 한계(Marginal) 자본과 노동, 장기와 단기 저량수요와 저량공급 사유재 / 클럽재 / 공유자원 / 공공재 GDP의 산출과 Y=C+I+G+NX 외환보유고 통화정책과 기준금리 주택담보대출과 LTV / DTI / DSR 지니 계수 - 소득 불평등의 측정 브레튼우즈 체제 / 달러와 기축통화[1] 페트로달러 체제 / 달러와 기축통화[2] 플라자 합의 / 일본의 ‘잃어버린 10년’ 2008년 미국발 글로벌 금융위기 국제수지=경상수지+자본수지규모의 경제 | 범위의 경제근면 혁명기저효과낙수효과 | 분수효과대공황 | 대침체 | 대봉쇄대분기(논쟁)디폴트 | 모라토리움레몬마켓모럴 해저드맬서스 트랩베어마켓/불마켓벤포드의 법칙배출권 거래 제도시장실패/정부실패실업/실업률인플레이션/디플레이션/스태그플레이션증자/감자좌파/우파카르텔쿠즈네츠 가설케인스폰지게임필립스곡선환율휘플지수/ABCC지수FED | FRB | FOMCJ커브효과 | 마샬-러너조건PBR | PER | EV/EBITDA | ROE | EPS [ 맨큐의 경제학 ] 1부. 서론 2부. 시장의 작동 원리 3부. 시장과 경제적 후생 4부. 공공경제학 5부. 기업행동과 산업조직 6부. 노동시장의 경제학 7부. 소비자선택이론과 미시경제학... 8부. 거시경제 데이터 9부. 장기 실물경제 10부. 화폐와 물가의 장기적 관계 11부. 개방경제의 거시경제학 12부. 단기 경기변동 13부. 책 말미에 [ 미시경제학 ] [미시.1] 소비자선택이론 [미시.2] 생산자선택이론 : 생산함수 [미시.3] 생산자선택이론 : 비용함수/공급함수 [미시.4] 노동시장의 수요/공급/균형 [미시.5] 일반균형이론과 후생경제학 [ 거시경제학 ] [거시.1] 국민소득결정이론 [거시.2] IS-LM 모형 [거시.3] AD-AS 모형 [거시.4] IS-LM-BP 모형 [ 기타 / 개인적인 생각 ] 공공경제학의 의의 금융시장론 요약 유동자산총액 결정 매커니즘 환율의 정의/환율-경상수지 결정모형 고용의 개념 및 측정상의 문제 주택가격결정 모형 다양한 국제 환경 협약이 우리나라... 소비함수(절대/상대/항상) 기준금리와 국채수익률의 관계 주식, 차트 보는 방법 2021년 경제전망 (개인의 견해) 비트코인과 가상화폐 (개인의 견해) 게임스탑(GME) 주가 폭등 사건 2022년 경제전망 (개인의 견해) 중위 연령 - 늙어가는 우리나라 2022년 엔저 효과 (개인의 견해) 2023년 경제전망 (개인의 견해) 2024년 경제전망 (개인의 견해)

HS LOG List of ECONOMY

Copyright © HS LOG