대푯값(Representative value)의 의미와 평균값(mean), 중앙값(median), 최빈값(mode)에 대해 알아보고, 평균의 함정에 대해 간단히 다루는 내용이다.

• 평균값만을 대푯값으로 생각하면, 평균의 함정에 빠질 수 있다는 것을 알리는 정도의 내용이다.
• 중학교 3학년 2학기에 배우는 내용의 일부이다. 단, 글쓴이는 30대에 알았다.
• 대푯값에 대해 더 자세한 내용이 필요하다면 : [ 나무위키에서 보기 ]

[1] 대푯값
대푯값은 어떤 데이터를 대표하는 값이다. 평균값, 중앙값, 최빈값, 백분위 수, 사분위 수, 절사평균 등을 사용할 수 있다.
 
[2] 평균값 / 중앙값 / 최빈값
평균값은 이미 알고 있다시피 n개의 변량을 모두 더하여 그 개수로 나누어 놓은 숫자이다. 중앙값(또는 중위수)은 n개의 값을 크기순으로 늘어놓았을 때 가장 가운데에 있는 숫자이다. 최빈값은 가장 빈번하게 등장하는 숫자를 의미한다.
 
[3] 평균의 함정
아래의 예를 통해서 평균의 함정에 대해 알아보자.

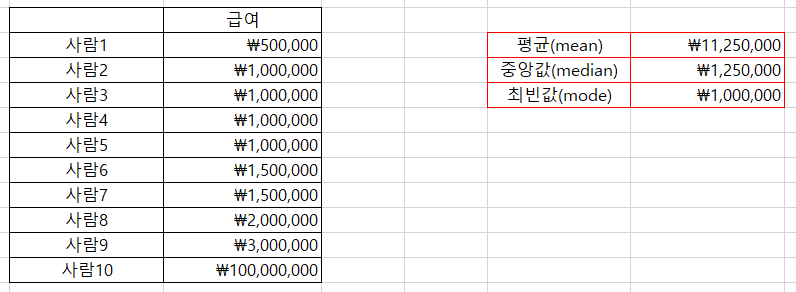
사람 10명의 급여에 대한 극단적인 데이터이다. 평균값(평균소득)은 11,250,000원, 중앙값(중위소득)은 1,250,000원이다. 위의 데이터에도 대푯값으로 평균값을 사용하는 경우가 있다. 데이터를 보지 않고 평균값만 들으면 마치 대부분의 사람이 11,250,000원을 버는 것 같은 착각에 빠지게 된다. 그런 경우가 바로 평균의 함정에 빠진 상황이다.

위의 데이터에는 평균값보다는 중앙값이 대푯값으로 더 적절할 수 있다.

• 실제로 정상적인 국가는 평균소득보다는 중위소득을 대푯값으로 생각하는 경우가 많다.
• 위와 같이 데이터의 양이 짝수개일 때는 중앙에 있는 2개의 값의 평균값을 중앙값으로 사용한다.
• 최빈값은 데이터의 수가 많고 중복된 값이 많을 때, 대푯값으로 사용하기에 좋다. 투표에서 대푯값으로 사용하기에 적절하다. 급여의 대푯값으로 최빈값을 사용하는 것은 적절하지 않다.

자료의 값 중에 매우 크거나 매우 작은 값이 있을 때는 대푯값으로 중앙값을 사용하는 것이 좋다. 평균의 함정에 빠지지 말자는 의미로 간단히 작성해보았다. Good!

현식로그 홈 기타(ETC) 목록

Copyright © HS LOG