생산자선택이론(theory of producer’s choice) – 생산함수(Production function)
2016년 05월 17일에 작성된 포스트입니다.

[ 짧고 쉬운 경제 ]
화폐, 통화, 그리고 신용창조수요/공급,소비자잉여/생산자잉여수요/공급의 가격탄력성
비교우위/절대우위, 보호무역/자유무역명목변수와 실질변수한계(Marginal)
자본과 노동, 장기와 단기저량수요와 저량공급사유재 / 클럽재 / 공유자원 / 공공재
GDP의 산출과 Y=C+I+G+NX인당 GDP와 노동소득분배율외환보유고
통화정책과 기준금리주택담보대출과 LTV / DTI / DSR지니 계수 - 소득 불평등의 측정
브레튼우즈 체제 / 달러와 기축통화[1]페트로달러 체제 / 달러와 기축통화[2]플라자 합의 / 일본의 ‘잃어버린 10년’
2008년 미국발 글로벌 금융위기
경제정책=재정정책+통화정책국제수지=경상수지+자본수지규모의 경제 | 범위의 경제근면 혁명기저효과낙수효과 | 분수효과대공황 | 대침체 | 대봉쇄대분기(논쟁)디폴트 | 모라토리움레몬마켓모럴 해저드맬서스 트랩베어마켓/불마켓벤포드의 법칙배출권 거래 제도시장실패/정부실패실업/실업률인플레이션/디플레이션/스태그플레이션증자/감자좌파/우파카르텔쿠즈네츠 가설케인스폰지게임필립스곡선환율휘플지수/ABCC지수FED | FRB | FOMCJ커브효과 | 마샬-러너조건PBR | PER | EV/EBITDA | ROE | EPS
[ 맨큐의 경제학 ]
1부. 서론2부. 시장의 작동 원리3부. 시장과 경제적 후생
4부. 공공경제학5부. 기업행동과 산업조직6부. 노동시장의 경제학
7부. 소비자선택이론과 미시경제학...8부. 거시경제 데이터9부. 장기 실물경제
10부. 화폐와 물가의 장기적 관계11부. 개방경제의 거시경제학12부. 단기 경기변동
13부. 책 말미에
[ 미시경제학 ]
[미시.1] 소비자선택이론 [미시.2] 생산자선택이론 : 생산함수
[미시.3] 생산자선택이론 : 비용함수/공급함수 [미시.4] 노동시장의 수요/공급/균형
[미시.5] 일반균형이론과 후생경제학
[ 거시경제학 ]
[거시.1] 국민소득결정이론[거시.2] IS-LM 모형
[거시.3] AD-AS 모형 [거시.4] IS-LM-BP 모형
[ 기타 / 개인적인 생각 ]
공공경제학의 의의금융시장론 요약유동자산총액 결정 매커니즘
환율의 정의/환율-경상수지 결정모형고용의 개념 및 측정상의 문제주택가격결정 모형
다양한 국제 환경 협약이 우리나라...소비함수(절대/상대/항상)기준금리와 국채수익률의 관계
주식, 차트 보는 방법2021년 경제전망 (개인의 견해)비트코인과 가상화폐 (개인의 견해)
게임스탑(GME) 주가 폭등 사건2022년 경제전망 (개인의 견해)중위 연령 - 늙어가는 우리나라
2022년 엔저 효과 (개인의 견해)2023년 경제전망 (개인의 견해)2024년 경제전망 (개인의 견해)


★ 본 포스트는 PC 에 최적화되어 있음

생산자선택이론

본 내용은 맨큐의 경제학 5부 기업행동과 산업조직의 확장판으로 생산자선택이론이며,
★★ 미시경제학에서는 대체적으로 소비자선택이론의 다음 편이다.
※ 때문에 미시경제학의 소비자선택이론을 이해한 뒤 보는 것이 더 좋다.

미시경제학 수업 내용을 중심으로 서승환교수님의 미시경제학,
위키백과, 네이버지식백과 등의 내용을 참고하여 작성하며,
생산자선택이론은 생산함수와 비용함수, 공급함수로 나누어 작성하며,
★★ 이번 포스트는 생산함수에 관련된 내용이다.

◆ 생산자선택이론(theory of producer’s choice) :
생산자는 가장 적은 비용으로 가장 많은 이익을 얻는 생산 계획을 따른다는 이론

※ 생산자선택이론의 비용함수와 공급함수는 다음 포스트를 참고하도록 한다.
생산자선택이론 – 비용함수/공급함수: 지금보기

■ 소비자선택이론과 생산자선택이론

(1) 생산자선택이론과 소비자선택이론의 유사점

  • 소비자선택이론이 예산제약하에 효용극대화를 이루는 합리적인 소비자를 가정한다면,
    생산자선택이론은 생산비제약하에 산출량을 최대로 하는 합리적인 생산자를 가정하며,
    등량곡선은 무차별곡선과, 예산제약선은 등비용선과 비슷한 개념으로 생각할 수 있다.

(2) 생산자선택이론과 소비자선택이론의 차이점

  • 소비자선택이론에서의 효용은 측정이 불가능하지만 산출량은 항상 측정이 가능하다.
    때문에 생산자선택이론은 항상 기수적 이론이 된다.
  • 소비자는 원하는 즉시 상품을 구입하여 소비할 수 있지만,
    생산자는 원하는 즉시 산출량을 증가시킬 수 없는 경우가 있다.
    특히 노동력(L)은 바로 증가시킬 수 있다고 판단하며, 자본(K)은 바로 증가시킬 수 없다고 본다.
    또 이에 따라서 단기에는 자본(K) 을 고정비용으로, 장기에는 자본(K) 을 가변비용으로 바라보며
    단기와 장기의 개념이 조금 다르다.
  • 소비자선택이론에서는 소득이 일정하게 주어졌다고 가정하기에 예산선은 움직이지 않지만
    기업의 경우 산출량을 변화시키려면 생산요소의 투입량도 변화시켜야 하므로 이에 따라 생산비가 변한다.
    때문에 합리적인 기업의 의사결정 목표는 이윤(총수입-총비용)을 극대화하는 것이 된다.

 

■ 단기생산함수

단기생산함수 : X = f(L) 혹은 X = f(L, \bar{K})(자본K는 고정)
※ 장기생산함수 : X = f(L, K)
※ 생산요소에 노동과 자본만 있다고 가정하여 표현(K는 자본, L은 노동)


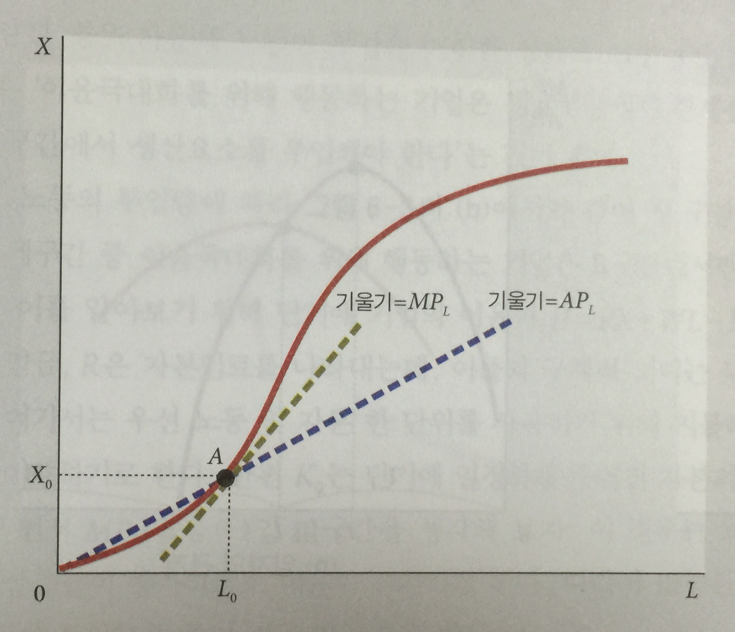
단기생산함수는 노동과 X재의 생산량으로 위와 같이 표현가능하다.
그리고 노동의 평균생산성(APL), 노동의 한계생산성(MPL)은 위 생산곡선의 평균값과 한계값이다.

AP_{L} = \frac{X}{L}
MP_{L} = \frac{\Delta X}{\Delta L}

물론 노동의 한계생산성은 궁극적으로 체감한다.
노동의 평균생산성(APL), 노동의 한계생산성(MPL) 을 그래프로 표현하면 아래와 같다.


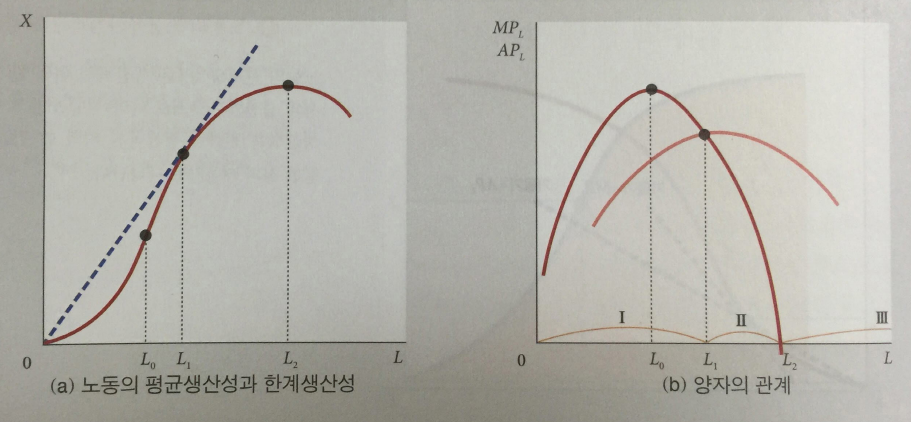
위 우측 그래프는 또한 생산의 3단계를 표현하고 있는데
I 단계는 APL 과 MPL 이 모두 증가하는 구간이며,
II 단계는 APL 과 MPL 이 모두 감소하는 구간,
III 단계는 MPL 이 0이 된 이후의 구간을 표현하고 있다.

우선 MPL 이 음(-)인 III 구간 에서는 노동의 투입량을 줄이면 산출량이 증가하는 구간이며,
MPL과 APL이 모두 증가 추세에 있는 I 구간에서는 노동의 투입량을 늘리면 산출량이 증가하는 구간이다.
결국 APL 과 MPL 이 양(+)의 값에서 감소 추세에 있는 II 단계에서 노동의 투입량을 결정하게 된다.

  • 기업의 이윤 = 총수입(TR) – 총비용(TC) 이며, 또한 다음과 같이 표현 가능하다.
    \pi = (P * X) - (WL + RK)
    이윤 = (가격 * 수량) – ((임금 * 노동) + (자본임료 * 자본))

■ 장기생산함수

장기생산함수 : X = f(L, K)(자본도 가변비용이 됨)

장기에도 APL 과 MPL 은 단기와 같이 정의되며,
자본의 평균생산성(APK)과 자본의 한계생산성(MPK)은 아래와 같이 정의된다.

AP_{L} = \frac{X}{L}
MP_{L} = \frac{\Delta X}{\Delta L}
AP_{K} = \frac{X}{K}
MP_{K} = \frac{\Delta X}{\Delta K}

역시 노동의 한계생산성(MPL), 자본의 한계생산성(MPK)은 궁극적으로 체감한다.

■ 등량곡선과 한계기술대체율

등량곡선(isoquant)이란 흔히 노동(L)과 자본(K)을 변수로 하는 좌표평면 상에서 나타내어지며,
동일한 양의 재화를 생산할 수 있는 노동과 자본의 조합을 연결한 곡선을 의미한다.
무차별곡선이 소비자이론에서 효용의 극대화를 달성하는 점을 찾기 위해 필요한 개념이라면,
등량곡선은 생산자이론에서 산출량의 극대화를 이루는 점을 찾기 위한 개념이라고 할 수 있다.

x축에 노동(L) 을 y축에 자본(K) 을 놓고 아래와 같은 등량곡선(isoquant)을 그릴 수 있다.


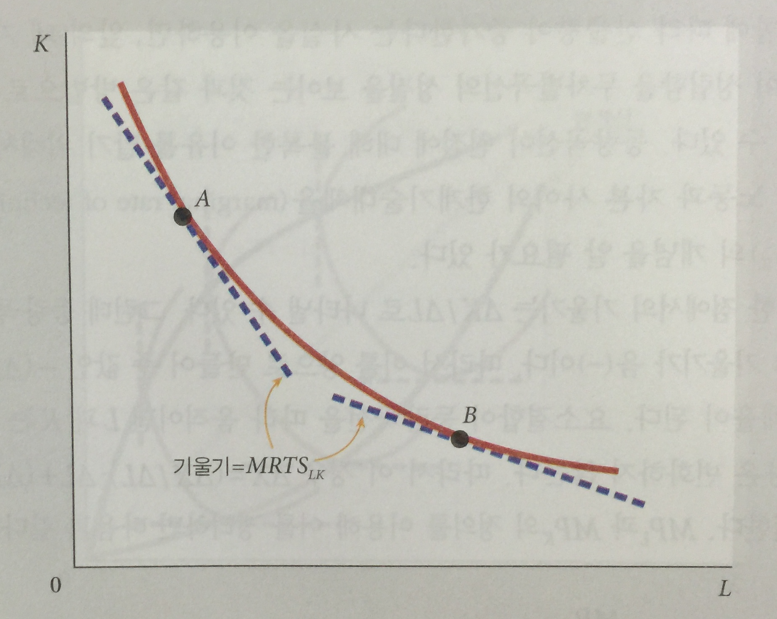
그리고 여기에서 한계기술대체율(marginal rate of Technical substitution)의 개념이 나온다.
노동을 추가로 한 단위 더 고용할 때 포기하여야 하는 자본량을 뜻하며,
등량곡선의 어느 한 점의 기울기를 양수(+)로 만들어준 값을 의미한다.
수식으로는 아래와 같다.

MRTS_{LK} = -\frac{\Delta K}{\Delta L} = \frac{MP_{L}}{MP_{K}}

 

■ 단기와 장기의 생산비제약


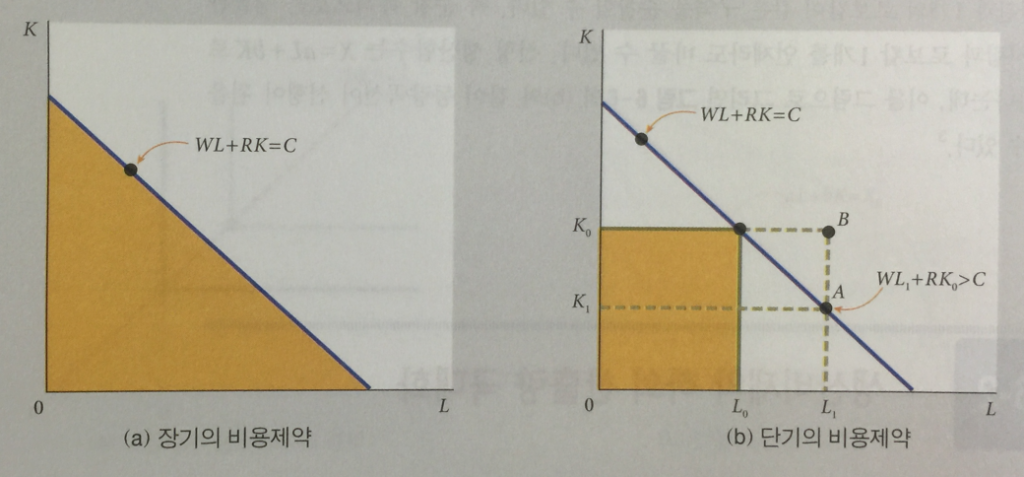
(1) 장기의 생산비제약과 등비용선

((임금 * 노동) + (자본임료 * 자본)) <= 총생산비용
WL + RK \leq C 에서 생산이 가능하다.

위 수식을 K 를 y축으로 L 을 x축으로 하여 보기 좋게 정리하면,
K = \frac{C}{R} - \frac{W}{R}L 이다.
절편은 C/R 이며, 기울기는 -(W/R) 이 된다.
위 좌측 그래프의 파란선과 노란색 부분 안이 투입가능 집합이며,
파란선이 등비용선이다.

(2) 단기의 생산비제약

단기에는 자본이 고정비용이기 때문에
자본이 K_{ 0 } 로 고정되었다고 가정했을 때
위 우측 그래프의 노란색 부분 안이 투입가능 집합이다.

WL+RK_{ 0 }\leq C (자본이 K_{ 0 } 로 고정되었다고 가정)
K_{ 0 }\leq K ( K_{ 0 } 보다 적은 자본(K)만이 투입 가능하다.)

 

■ 생산비 제약하에 산출량 극대화

(1) 단기의 생산비제약 하의 산출량 극대화



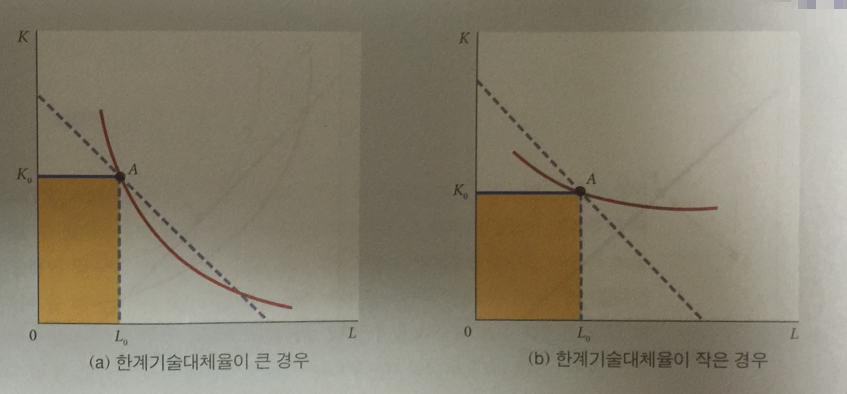
단기에 생산비제약 하의 산출량을 극대화 하는 지점은
주어진 K_{ 0 } 를 자본 투입량으로 결정하고,
사용 가능한 생산비 중 자본임료 지불액을 제외한 나머지로 L 을 구입해
L= \frac {C-RK_{0}}{ W} 로 결정하는 것이 최적이다.

위 그래프에서 A 지점이 되며,
단기의 경우 (장기인 경우에 나타나는) 등비용선이 등량곡선과 접한다는 보장은 없다.

(2) 장기의 생산비제약 하의 산출량 극대화


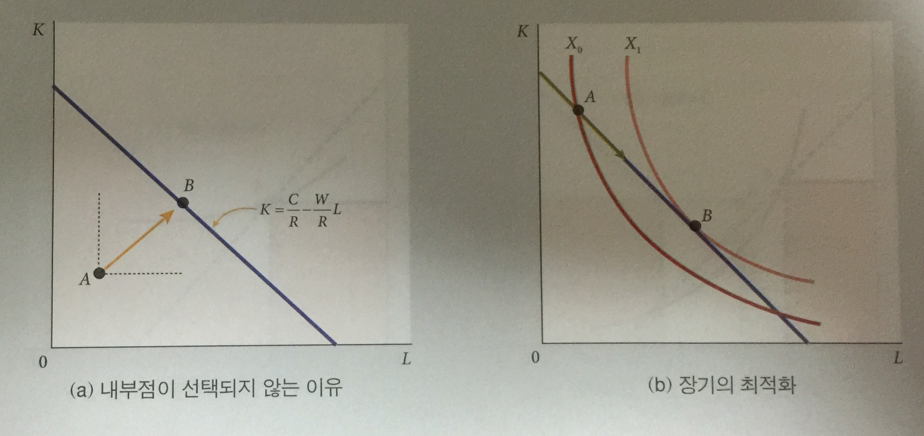
장기에 생산비제약 하의 산출량을 극대화 하는 지점은 투입 가능 집합 중 등비용선에서 결정된다.

  • 위 좌측 그래프처럼 내부점 A를 선택했을 경우 노동과 자본의 투입량을 증가시켜
    등비용선상의 B 지점으로 이동하여 산출량을 증가시킬 수 있기 때문이다.

결국 등비곡선에서 산출량 극대화를 이룰 수 있는 점은 바로 등량곡선과 접하는 지점이다.

  • 등량곡선은 우상단에 있을 수록 더 많은 산출량을 만들어낼 수 있는 노동/자본 조합이며,
    때문에 위 오른쪽 그래프에서 보다시피 등비용선과 등량곡선이 만나는 지점이
    같은 비용에 가장 많은 산출량을 만들어낼 수 있는 지점이다.

그리고 등비용선의 기울기는 -(W/R) 이고,
등량곡선의 한점에서의 기울기를 양(+)으로 만들어준 값이 MRTS_{LK} 이므로
장기 생산비제약 하의 산출량 극대화 조건은 아래와 같이 표현할 수 있다.
★★ MRTS_{LK} = \frac{W}{R}

또한 MRTS_{LK} = \frac{MP_{L}}{MP_{K}}= \frac{W}{R} 이므로
\frac{MP_{L}}{W} = \frac{MP_{K}}{R} 이다.
이 조건은 화폐 1원당 ★★ 한계생산물 균등의 법칙을 나타내며, 산출량 극대화를 달성하는 지점을 뜻한다.

(3) 장기와 단기의 비교

결국 장기에는 등비용선이 등량곡선과 접하는 지점을 택할 수 있지만,
단기에서의 최적 선택은 그렇지 않을 수 있기 때문에 장기가 더 효율적이다.

  • 등비용선과 등량곡선이 접하는 지점은 동일한 비용 중 가장 산출량이 높은 지점이기에 당연하다.

■ 결합생산

결합생산

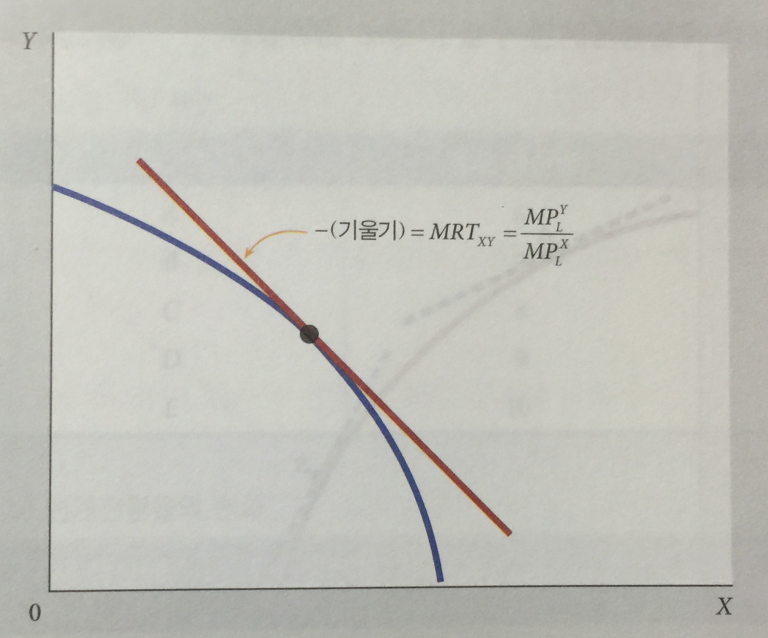
지금까지 고려된 생산함수는 여러 종류의 생산요소를 이용하여 한 가지 생산물을 만들어내는 경우이며,
결합생산(joint production)은 생산과정에서 여러가지 생산물을 얻는 것을 뜻한다.
노동(L) 만을 투입해 X재와 Y재를 만드는 만들어내는 함수를 보자면 아래와 같다.

L = h(X,Y)

그리고 아래와 같이 표현할 수 있다.

L = L_{x}+L_{y}
(노동 = X재 생산에 투입한 노동 + Y재 생산에 투입한 노동)

그리고 위 생산가능함수를 (X,Y) 평면에 그린 것이 생산가능곡선이며 위의 그래프와 같다.
또한 생산가능곡선은 다음과 같은 성질을 만족시킨다.

  1. 생산가능 곡선은 우하향한다.
  2. 노동의 투입량이 많아질수록 생산가능곡선은 원점에서 멀어진다.
  3. 생산가능곡선은 원점에 대해 오목하다.

위 생산가능곡선이 원점에 대해 오목한 이유를 알아보기 위해
X와 Y 의 한계전환율(marginal rate of transformation, MRT)의 개념을 알아보자면,
한계전환율이란 생산가능곡선 위의 한 점에서의 기울기를 구해 양수(+)로 만든 값이다.

MRT_{xy} = -\frac{\Delta Y}{\Delta X} 이며,

또한 MRT_{xy} = \frac{MP_{L}^{Y}}{MP_{L}^{X}} 이다.

생산가능곡선이 원점에 대해 오목한 이유로 한계생산성 체감의 법칙과 함께
이질적인(질이 다른) 노동(heterogeneous labour)을 들 수 있다.



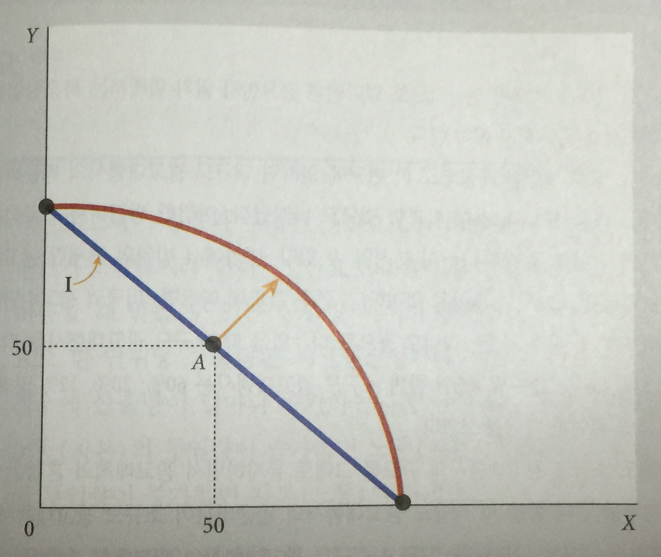
또한 여러가지 산출물을 동시에 생산하는 경우의 생산비가 그 산출물들을 따로 생산하는 경우보다
더 적다면 범위의 경제(economies of scope) 가 존재한다고 한다.
※ 예를 들어 휘발유를 얻기 위해 원유를 정제하는 과정에서 등유도 같이 얻는 것 같은 경우
※ 수직적 통합(verical integration)이 이루어진(중간재, 소비재 모두 생산) 경우에도 존재 가능

위 그래프를 통해 보자면
범위의 경제가 없다면 X재와 Y재를 동시에 50단위씩 생산해 생산비가 100인 경우로 볼 수 있다.
범위의 경제가 있다면 X재와 Y재를 50단위씩 생산하면 따로 생산하는 경우보다 생산비가 감소한다.
따라서 100의 생산비로 X재와 Y재를 동시에 생산하면 X재와 Y재의 생산량을
모두 A가 나타내는 것보다 증가시킬 수 있다.
※ 비용으로 보았을 때, 범위의 경제가 있다면 C(X,Y) < C(X) + C(Y) 이다.

생산자선택이론의 비용함수와 공급함수는 다음편을 참고하도록 한다.
◆ 생산자선택이론 – 비용함수/공급함수: 지금보기


★ 본 포스트는 PC 에 최적화되어 있음


[ 짧고 쉬운 경제 ]
화폐, 통화, 그리고 신용창조수요/공급,소비자잉여/생산자잉여수요/공급의 가격탄력성
비교우위/절대우위, 보호무역/자유무역명목변수와 실질변수한계(Marginal)
자본과 노동, 장기와 단기저량수요와 저량공급사유재 / 클럽재 / 공유자원 / 공공재
GDP의 산출과 Y=C+I+G+NX인당 GDP와 노동소득분배율외환보유고
통화정책과 기준금리주택담보대출과 LTV / DTI / DSR지니 계수 - 소득 불평등의 측정
브레튼우즈 체제 / 달러와 기축통화[1]페트로달러 체제 / 달러와 기축통화[2]플라자 합의 / 일본의 ‘잃어버린 10년’
2008년 미국발 글로벌 금융위기
경제정책=재정정책+통화정책국제수지=경상수지+자본수지규모의 경제 | 범위의 경제근면 혁명기저효과낙수효과 | 분수효과대공황 | 대침체 | 대봉쇄대분기(논쟁)디폴트 | 모라토리움레몬마켓모럴 해저드맬서스 트랩베어마켓/불마켓벤포드의 법칙배출권 거래 제도시장실패/정부실패실업/실업률인플레이션/디플레이션/스태그플레이션증자/감자좌파/우파카르텔쿠즈네츠 가설케인스폰지게임필립스곡선환율휘플지수/ABCC지수FED | FRB | FOMCJ커브효과 | 마샬-러너조건PBR | PER | EV/EBITDA | ROE | EPS
[ 맨큐의 경제학 ]
1부. 서론2부. 시장의 작동 원리3부. 시장과 경제적 후생
4부. 공공경제학5부. 기업행동과 산업조직6부. 노동시장의 경제학
7부. 소비자선택이론과 미시경제학...8부. 거시경제 데이터9부. 장기 실물경제
10부. 화폐와 물가의 장기적 관계11부. 개방경제의 거시경제학12부. 단기 경기변동
13부. 책 말미에
[ 미시경제학 ]
[미시.1] 소비자선택이론 [미시.2] 생산자선택이론 : 생산함수
[미시.3] 생산자선택이론 : 비용함수/공급함수 [미시.4] 노동시장의 수요/공급/균형
[미시.5] 일반균형이론과 후생경제학
[ 거시경제학 ]
[거시.1] 국민소득결정이론[거시.2] IS-LM 모형
[거시.3] AD-AS 모형 [거시.4] IS-LM-BP 모형
[ 기타 / 개인적인 생각 ]
공공경제학의 의의금융시장론 요약유동자산총액 결정 매커니즘
환율의 정의/환율-경상수지 결정모형고용의 개념 및 측정상의 문제주택가격결정 모형
다양한 국제 환경 협약이 우리나라...소비함수(절대/상대/항상)기준금리와 국채수익률의 관계
주식, 차트 보는 방법2021년 경제전망 (개인의 견해)비트코인과 가상화폐 (개인의 견해)
게임스탑(GME) 주가 폭등 사건2022년 경제전망 (개인의 견해)중위 연령 - 늙어가는 우리나라
2022년 엔저 효과 (개인의 견해)2023년 경제전망 (개인의 견해)2024년 경제전망 (개인의 견해)

- hyunsik.me -

관련 있는 글

  • IS-LM 모형
  • [H-경제] 주택가격결정 모형
  • [경제 용어] J커브 효과(J-curve effect)와 마샬-러너 조건(Marshall-Lerner condition)
  • [경제 용어] 낙수효과와 분수효과
  • [짧고 쉬운 경제] 자본과 노동, 장기와 단기는 무엇인가?
  • [짧고 쉬운 경제] 주택담보대출, 그리고 LTV, DTI, DSR은 무엇인가?
  • 국민소득결정 이론(theory of income determination)
  • 맨큐의 경제학 정리 By H Log – 5부. 기업행동과 산업조직
  • 맨큐의 경제학 정리 By H Log – 6부. 노동시장의 경제학
  • 맨큐의 경제학 정리 By H Log – 7부. 소비자 선택 이론과 미시경제학의 새로운 영역
  • 맨큐의 경제학 정리 By H Log – 9부. 장기 실물경제
  • 생산자선택이론(theory of producer’s choice) – 비용함수(cost function) / 공급함수(supply function)
  • 소비자선택이론(theory of consumer choice)
  • 소비함수(consumption function) – 절대소득가설, 생애주기가설, 상대소득가설, 항상소득가설
  • 일반균형이론(general equilibrium theory)과 후생경제학(welfare economics)

    • 현식로그 홈 경제(Economy) 목록

    Copyright © HS LOG
    Published on 5월 17, 2016 Filed under: Economy; Tagged as: , , , ,

    No Comments

    방문해 주셔서 감사합니다. 답글을 남겨주시면 잊지 못할 것입니다.

    현식로그 홈 경제(Economy) 목록

     
    이 글의 방문자수는 36,324 입니다. (젯팩이 측정)